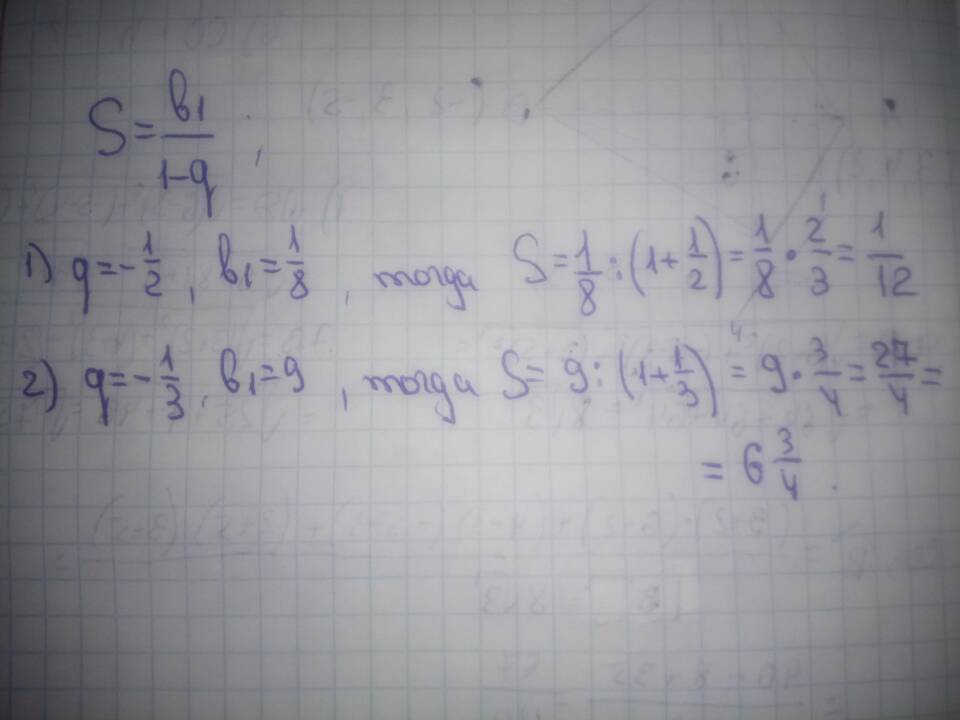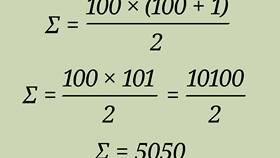Бесконечно убывающая геометрическая прогрессия - это последовательность чисел, где каждый последующий член получается умножением предыдущего на постоянное число q (знаменатель), причем |q| < 1.
Содержание
Определение бесконечно убывающей прогрессии
Бесконечно убывающая геометрическая прогрессия - это последовательность чисел, где каждый последующий член получается умножением предыдущего на постоянное число q (знаменатель), причем |q| < 1.
Формула суммы бесконечно убывающей прогрессии
| Формула | S = a₁ / (1 - q) |
| Где: |
|
Условия применения формулы
- Прогрессия должна быть геометрической
- Знаменатель q по модулю меньше 1
- Число членов прогрессии стремится к бесконечности
Пошаговый алгоритм вычисления
- Определите первый член прогрессии (a₁)
- Найдите знаменатель прогрессии (q)
- Убедитесь, что |q| < 1
- Подставьте значения в формулу S = a₁ / (1 - q)
- Выполните вычисления
Пример расчета
| Дано: | 8, 4, 2, 1, 0.5, ... |
| Решение: |
|
Практическое применение
Где используются такие расчеты
- В экономике - расчет бесконечных рент
- В физике - моделирование затухающих процессов
- В компьютерных науках - анализ алгоритмов
- В теории вероятностей
Математическое обоснование
Формула выводится из суммы конечной геометрической прогрессии Sₙ = a₁(1 - qⁿ)/(1 - q), при n → ∞ и |q| < 1, qⁿ → 0.
Особые случаи и ограничения
| Ситуация | Результат |
| |q| ≥ 1 | Сумма не существует (расходится) |
| q = 0 | S = a₁ |
| a₁ = 0 | S = 0 |
Проверка сходимости ряда
- Вычислите несколько первых членов прогрессии
- Определите знаменатель q
- Проверьте выполнение условия |q| < 1
- Только при выполнении условия применяйте формулу
